ja.wikipedia.org
数学的に公民を見るシリーズができた。前回は、
ということだろう。
概要
二大政党制を想定し、支持者の数で不利であろう A 党がそうでない B 党に勝つための選挙区の区分けを行いたい。
選挙のルールと勝敗
- 地区
- 各地区は A 党の支持者と B 党の支持者からなる。
- 選挙区
- いくつかある地区をいくつかに区切って選挙区を作る。このとき、おのおのの選挙区は飛び地を持たないようにする。
- 各選挙区について、それに属する地区の各党の支持者数を党ごとに合算する。
- 選挙
- 選挙区ごとに、より多くの支持者数がいる党がその選挙区を獲得する。最終的に他党より多くの選挙区を獲得できた党が選挙において勝利する。
ja.wikipedia.org
ゲリマンダリングのシミュレーション
方法
あり得る区分けを列挙し、それぞれについて勝敗を評価する。
また、それについてはグラフ理論を用いるが、あまり一般的ではないかもしれない用語を定義したい。
- グラフの分割・連結分割
- グラフ $G$ の頂点集合 $V(G)$ の分割 $\{V_j\}$ を考える。このとき、$\{V_j\}$ によって得られる $G$ の誘導部分グラフの集合 $\{G[V_j]\}$ を $G$ の分割 (partition) と呼ぶ。
- とくに、分割 $\{G[V_j]\}$ のすべての元が連結であるとき、連結分割 (connected partition) と呼ぶ。
連結分割は仮想的に適当な辺を除去することで仮想的な連結成分を作るイメージ。
グラフ理論の基本的なところは以下参照。
www.momoyama-usagi.com
www.momoyama-usagi.com
区分け
地区を頂点とし、地区どうしの隣接関係を辺としたグラフ $G(V)$ を作り、そのグラフを $N$ 個に連結分割した $\{G[V_j]\}$ を考える。$\abs{\{j\}} = N$ である。この連結分割の各元に選挙区を紐付けることで $N$ 個の選挙区を得る。
勝敗
- 地区のスコア
- 各地区について A 党の支持者数から B 党の支持者数を引いた数をスコアと呼ぶことにし、各頂点 $v_i \in V$ にスコア $S(v_i)$ を紐付ける。
- 選挙区の勝ち点
$G[V_j]$ に属する頂点のスコアの和 $S_j$ を求める。すなわち、$$S_j = \sum_{v_i \in V_j} S(v_i)$$である。さらに、これに基づいてそれぞれの選挙区 $j$ に勝ち点 $P_j$ を次のように割り振ることにする。 $$P_j = \begin{cases} 1 & (S_j > 0) \\ 0 & (S_j = 0) \\ -1 & (S_j < 0) \end{cases}$$
- 選挙の勝敗
- 選挙区ごとの勝ち点の総和 $\sum_j P_j$ が正であれば A 党の勝利とする。
具体例
15 個の地区を用意した。次のグラフに示す。
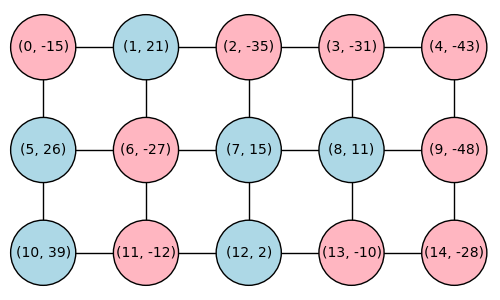
各頂点 $v_i$ には地区の番号とスコアが $(i, S(v_i))$ という対として記載されており、赤い頂点は $S(v_i) < 0$、青い頂点は $S(v_i) > 0$ であること示している。各頂点のスコアは番号順に、$$
\begin{align} \{S(v_i)\} =& -15, 21, -35, -31, -43, \\
& 26, -27, 15, 11, -48, \\
& 39, -12, 2, -10, -28
\end{align}
$$となっており、その和は $-135$ である。また、赤い頂点は 9 個、青い頂点は 6 個である。すなわち、
- 全体で見ると A 党の支持者数は B 党を下回っている
- A 党支持者の多い地区のほうが B 党支持者の多い地区より少ない
という A 党劣勢を覆していくのが目的。
今回は選挙区を 3 つ設けたい。そういったグラフの分割方法は 5368 通りあるらしい。勝ち点の和ごとの内訳を次の表に示す。
| 勝ち点の和 | 分割方法の数 |
|---|---|
| 1 | 621 |
| 0 | 25 |
| -1 | 3411 |
| -2 | 42 |
| -3 | 1269 |
| 計 | 5368 |
ゲリマンダーが成功する組合せが 621 通りあることを示している。
成功例

濃い色の辺で結ばれている部分グラフが選挙区に対応していると思ってほしい。
この例は地区の番号の分割が、$$\{\{0, 5, 10, 11, 12, 13\}, \{1, 6, 7\}, \{2, 3, 4, 8, 9, 14\}\} $$である場合である。すなわち、$$(V_0, V_1, V_2) = (\{v_0, v_5, v_{10}, v_{11}, v_{12}, v_{13}\}, \{v_1, v_6, v_7\}, \{v_2, v_3, v_4, v_8, v_9, v_{14}\}) $$によるグラフの分割 $\{G[V_0], G[V_1], G[V_2]\}$ を考えている。このとき、選挙区ごとのスコアの和は、$$(S_0, S_1, S_2) = (30, -174, 9) $$となり、勝ち点は$$(P_0, P_1, P_2) = (1, -1, 1) $$である。よって、勝ち点の和 $P_0 + P_1 + P_2$ が $1$ であるから、A 党が大逆転勝利を遂げる。
また、次に図示する区分けは自明な成功例といえる。

互いに隣接する有利な地区のみからなる勝ち点 $1$ が必然な選挙区の数が過半数を占めた時点で勝利する、トリビアルな区分けである。今回は一票の格差やらの平等性を無視したので、こういうのもアリ。
失敗例

また、$$(V_0, V_1, V_2) = (\{v_0, v_1, v_2, v_3, v_5\}, \{v_4, v_6, v_7, v_8, v_9, v_{14}\}, \{v_{10}, v_{11}, v_{12}, v_{13}\}) $$による分割では、選挙区ごとのスコアの和は、$$(S_0, S_1, S_2) = (-120, -34, 19) $$となり、勝ち点は$$(P_0, P_1, P_2) = (-1, -1, 1) $$であるから、勝ち点の和が $-1$ であり、A 党が敗北したのでゲリマンダー失敗である。
コード
今回のシミュレーションで使った SageMath のコード。与えるグラフが大きかったりすると終わらない。
def connected_partition_iterator(G, k): """ Partition G into `k` connected induced subgraphs. """ if G.order() == 0 or k > G.order(): return root = G.vertices()[0] for csg_with_root in filter( lambda sg: root in sg, G.connected_subgraph_iterator(k=G.order() - k + 1), ): sg_opposite = G.subgraph(set(G) - set(csg_with_root)) m = sg_opposite.connected_components_number() if m == k - 1: yield [csg_with_root] + [ G.subgraph(cc) for cc in sg_opposite.connected_components(sort=False) ] elif m < k - 1: for parts in connected_partition_iterator(sg_opposite, k - 1): yield [csg_with_root] + [G.subgraph(part) for part in parts] def custom_show(G, supergraph=None): excluded_edges = set(supergraph.edges()) - set(G.edges()) if supergraph else {} g = supergraph or G g.show( fig_tight=False, figsize=[5, 3], vertex_size=2200, vertex_colors={ "white": list(filter(lambda v: v[1] == 0, g)), "lightblue": list(filter(lambda v: v[1] > 0, g)), "lightpink": list(filter(lambda v: v[1] < 0, g)), }, edge_colors={"gainsboro": excluded_edges}, ) def show_partition(partition, supergraph): custom_show( supergraph.subgraph( edges=set.union(*[set(part.edges()) for part in partition]) ), supergraph, ) g = graphs.Grid2dGraph(3, 5) scores = [-15, 21, -35, -31, -43, 26, -27, 15, 11, -48, 39, -12, 2, -10, -28] assert g.order() == len(scores) g.relabel(enumerate(scores)) n = 3 stats = {} custom_show(g) partitions = [*connected_partition_iterator(g, n)] # show_partition(partitions[5152], g) for i, partition in enumerate(partitions): assert len(partition) == n scores_by_part = [sum([v[1] for v in part]) for part in partition] result = sum(sgn(s) for s in scores_by_part) if not result in stats: stats[result] = [] stats[result].append( ( sorted( [sorted({v[0] for v in part}) for part in partition], key=lambda a: a[0] ), scores_by_part, i, ) ) print("Stats:", [(k, len(stats[k])) for k in sorted(stats.keys(), reverse=True)]) print("Details: <partition> <scores> <points> <#>") for k in sorted(stats.keys(), reverse=True): for p, s, i in stats[k]: print(p, s, k, "#%d" % i)
