序
直角二等辺三角形な三角定規に分度器の機能が載っていれば小学生の算数道具が減るのではないかという発想。すなわち通常の半円状の分度器の $0\degree$ から $90\degree$ の部分と $90\degree$ から $180\degree$ の部分を直線状にするには目盛り幅をどうすればよいのかということを考える。ここでは $0\degree$ から $90\degree$ の部分のみを考える。
ある角度における $0\degree$ からの長さ
$\mathrm{OA}=\mathrm{OB}=1$ な直角二等辺三角形 $\mathrm{OAB}$ を考える。
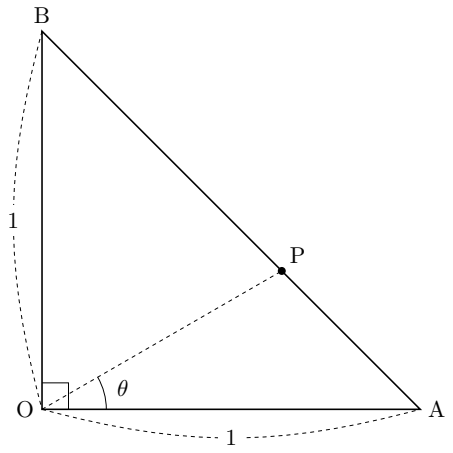
辺 $\mathrm{AB}$ 上に点 $\mathrm{P}$ をとり、$\theta \triangleq \angle \mathrm{AOP}$ とおくと、\begin{empheq}[left=\empheqlbrace]{align}
\triangle \mathrm{OAP} &= \frac{1}{2} \mathrm{OA} \cdot \mathrm{OP} \sin{\angle \mathrm{AOP}} = \frac{1}{2} \mathrm{OP} \sin{\theta} \\
\triangle \mathrm{OBP} &= \frac{1}{2} \mathrm{OB} \cdot \mathrm{OP} \sin(\frac{\pi}{2} - \angle \mathrm{AOP}) = \frac{1}{2} \mathrm{OP} \cos{\theta}
\end{empheq}である。$\triangle \mathrm{OAP} + \triangle \mathrm{OBP} = \triangle \mathrm{OAB} = 1/2$ ゆえ、\[
\frac{1}{2} \mathrm{OP} (\sin{\theta}+ \cos{\theta}) = \frac{1}{2}\]より、\begin{align}
\mathrm{OP}
&=\frac{1}{\sin{\theta}+ \cos{\theta}} \\
&= \frac{1}{\sqrt{2} \sin(\theta + \frac{\pi}{4})}
\end{align}となるから、\[\triangle \mathrm{OAP} = \frac{\sin{\theta}}{2\sqrt{2} \sin(\theta + \frac{\pi}{4})}\]と表せる。いっぽうで、\[\triangle \mathrm{OAP} = \frac{1}{2} \mathrm{OA} \cdot \mathrm{AP} \sin{\angle \mathrm{OAP}} = \frac{1}{2\sqrt{2}} \mathrm{AP}\]とも表せるから、\[\frac{\sin{\theta}}{2\sqrt{2} \sin(\theta + \frac{\pi}{4})} = \frac{1}{2 \sqrt{2}} \mathrm{AP}\]が成り立ち、\[\mathrm{AP} = \frac{\sin{\theta}}{\sin(\theta + \frac{\pi}{4})}\]である。
目盛り幅
さて、正の数 $t$ および非負整数 $k$ について、辺 $\mathrm{AB}$ 上の点 $\mathrm{P}_k$ が $\angle \mathrm{AOP}_k = kt$ を満たすものとする。
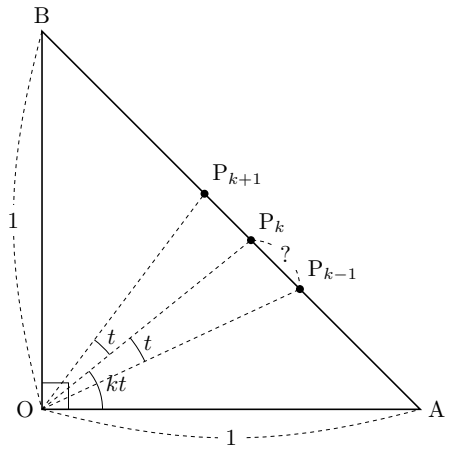
このとき、上記の議論より、\[\mathrm{AP}_k= \frac{\sin{kt}}{\sin(kt + \frac{\pi}{4})}\]が成り立つ。ゆえに、$kt \leq \pi/2$ であるとき、\begin{align}
\mathrm{P_k P_{k-1}}
&= \mathrm{AP}_k - \mathrm{AP}_{k-1} \\
&= \frac{\sin{kt}}{\sin(kt + \frac{\pi}{4})} - \frac{\sin{(k-1)t}}{\sin((k-1)t + \frac{\pi}{4})} \\
&= \frac{\sin((k-1)t + \frac{\pi}{4}) \sin{kt} - \sin(kt + \frac{\pi}{4})\sin{(k-1)t}}{\sin(kt + \frac{\pi}{4}) \sin((k-1)t + \frac{\pi}{4})} \\
&= \frac{\sin{kt} \cos{(k-1)t} - \cos{kt} \sin{(k-1)t}}{\sqrt{2} \sin(kt + \frac{\pi}{4}) \sin((k-1)t + \frac{\pi}{4})} \\
&= \frac{\sin{t}}{\sqrt{2} \sin(kt + \frac{\pi}{4}) \sin((k-1)t + \frac{\pi}{4})}
\end{align}である。この分母を変形したバージョンとして、\begin{align}
\mathrm{P_k P_{k-1}}
&= \frac{\sin{t}}{\sqrt{2} \cdot \frac{1}{2} \qty(-\cos((2k-1)t + \frac{\pi}{2}) + \cos{t})} \\
&= \frac{\sqrt{2}\sin{t}}{\sin{(2k-1)t} + \cos{t}}
\end{align}が得られる。また、分子を変形したバージョンとして、\begin{align}
\mathrm{P_k P_{k-1}}
&= \frac{\sin( (kt + \frac{\pi}{4}) - ((k-1)t + \frac{\pi}{4}) )}{\sqrt{2} \sin(kt + \frac{\pi}{4}) \sin((k-1)t + \frac{\pi}{4})} \\
&= \frac{\sin(kt + \frac{\pi}{4}) \cos((k-1)t + \frac{\pi}{4}) - \cos(kt + \frac{\pi}{4}) \sin((k-1)t + \frac{\pi}{4})}{\sqrt{2} \sin(kt + \frac{\pi}{4}) \sin((k-1)t + \frac{\pi}{4})} \\
&= \frac{1}{\sqrt{2}} \qty( \cot((k-1)t + \frac{\pi}{4}) - \cot(kt + \frac{\pi}{4}) ) \\
&= \frac{1}{\sqrt{2}} \qty( \tan(kt - \frac{\pi}{4}) - \tan((k-1)t - \frac{\pi}{4}) )
\end{align}が得られる。これは $\mathrm{O}$ を中心に全体を $-\pi/4$ 回転した図を想像するとわかりやすいかも、というか、これを出発点にしたほうがよかったかも。

$t=\pi/180$ とすると、辺 $\mathrm{AB}$ 上に $0\degree$ から $90\degree$ までの $1\degree$ 刻みの目盛りを割り振ったときの目盛りの間隔がわかる。すなわち $(k-1)\degree$ から $k\degree$ の間の間隔は $\mathrm{P_k P_{k-1}}$ であって、上記の各バージョンで表せば、\begin{align}
\mathrm{P_k P_{k-1}}
&= \frac{\sin{\frac{\pi}{180}}}{\sqrt{2} \sin(\frac{k \pi}{180} + \frac{\pi}{4}) \sin(\frac{(k-1) \pi}{180} + \frac{\pi}{4})} \\
&= \frac{\sqrt{2}\sin{\frac{\pi}{180}} }{\sin{\frac{(2k-1) \pi}{180}} +\cos{\frac{\pi}{180}}} \\
&= \frac{1}{\sqrt{2}} \qty( \tan(\frac{k \pi}{180} - \frac{\pi}{4}) - \tan(\frac{(k-1) \pi}{180} - \frac{\pi}{4}) )
\end{align}となる。
蛇足
一般に $n$ を正の整数として $t=\pi/2n$ のとき、\[\sum_{k=1}^n \mathrm{P_k P_{k-1}} = \mathrm{AB} = \sqrt{2}\]が成り立つが、\begin{align}
&\phantom{{}={}}\sum_{k=1}^n \frac{1}{\sqrt{2}} \qty( \tan(\frac{k\pi}{2n} - \frac{\pi}{4}) - \tan(\frac{(k-1)\pi}{2n} - \frac{\pi}{4}) ) \\
&= \frac{1}{\sqrt{2}} \qty( \tan(\frac{n\pi}{2n} - \frac{\pi}{4}) - \tan(\frac{0\pi}{2n} - \frac{\pi}{4}) ) \\
&= \frac{1}{\sqrt{2}} \qty( \tan{\frac{\pi}{4}} - \tan(- \frac{\pi}{4}) ) \\
&= \sqrt{2}
\end{align}が望遠鏡和より確認できる。
また、\[\sum_{k=1}^n \frac{\sin{\frac{\pi}{2n}}}{\sin{\frac{(2k-1) \pi}{2n}} +\cos{\frac{\pi}{2n}}} = 1\]なる三角関数の和に関する非自明な関係式が得られる。これは Dirichlet 核\[D_k(x) \triangleq \frac{\sin{\qty(k + \frac{1}{2}) x}}{\sin{\frac{x}{2}}}\]を用いて、
\[\sum_{k=1}^n \frac{1}{D_{k-1}(\frac{\pi}{n}) + \cot{\frac{\pi}{2n}}} = 1\]とも表せるが、ここまでやる意味は不明。