
ハノイの塔というパズルゲームがある。これは 3 本の柱 $A,B,C$ と穴の開いた $n$ 枚の円盤から構成される。ゲーム開始状態では柱 $A$ にすべての円盤が刺さっている。これらのすべての円盤を以下のルールに従って、柱 $C$ に移動させるとゲームは完了する。
- 開始状態から一貫して、どの柱についても任意の円盤の上にはそれよりも小さい円盤だけがある
- 1 回の手順ではいずれかの柱の最上部の円盤 1 つを別のいずれかの柱に移動させる
これに従ってゲームを進めるとき、最短手順は $2^n-1$ 回であることが知られている。
また、この最短手順で攻略するための再帰的なアルゴリズムが知られている。
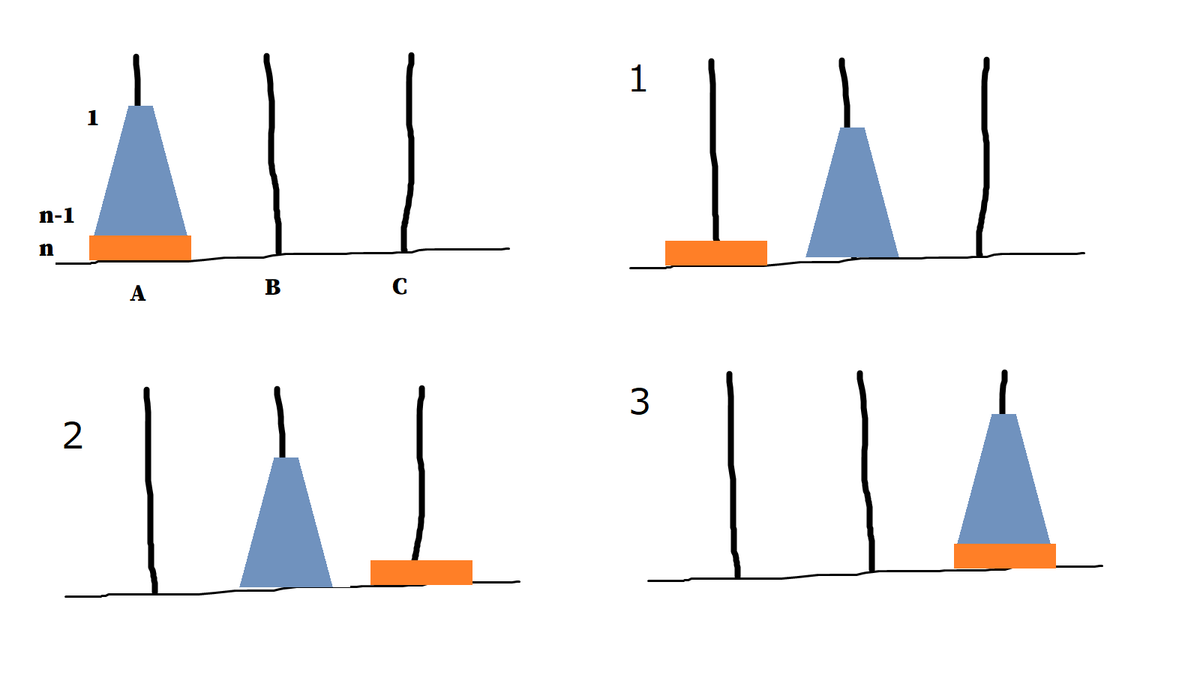
- 柱 $A$ の 上部 $n-1$ 段を柱 $B$ に移動する
- 柱 $A$ に残った円盤 $n$ を柱 $C$ に移動する
- 柱 $B$ の $n-1$ 段を柱 $C$ に移動する
これを下に図示する。
問題
上記の最短手順で $n$ 段のハノイの塔を攻略するとき、
- $k$ 番目に小さい円盤を $k$ とする(最小の円盤が $1$、最大の円盤が $n$)
- 各手順について、円盤 $k$ の移動先の柱に点数 $k$ が加算される
- 最初の段階で各柱の点数は $0$ である
という条件のもとで攻略終了時の柱 $A, B, C$ の点数をそれぞれ $a_n, b_n, c_n$ として、それらを求めよ。
方針
- 柱 $A$ の 上部 $n-1$ 段を柱 $B$ に移動する
- 柱 $A$ に残った円盤 $n$ を柱 $C$ に移動する
- 柱 $B$ の $n-1$ 段を柱 $C$ に移動する
以上の 3 段階に分割して考える。
ステップ 1 では、柱 $B$ と柱 $C$ の役割が入れ替わっているので、$A$ に $a_{n-1}$ 点、$B$ に $c_{n-1}$ 点、$C$ に $b_{n-1}$ 点、それぞれ加算される。
ステップ 2 では $C$ に $n$ 点加算される。
ステップ 3 では、柱 $A$ と柱 $B$ の役割が入れ替わっているので、$A$ に $ b_{n-1}$ 点、$B$ に $a_{n-1}$ 点、$C$ に $c_{n-1}$ 点、それぞれ加算される。
これらを合算すると、$$
\begin{empheq}[left=\empheqlbrace]{align}
a_n &= a_{n-1}+b_{n-1} \\
b_n &= a_{n-1}+c_{n-1} \\
c_n &= b_{n-1}+c_{n-1}+n
\end{empheq}
$$という連立漸化式が得られる。また、$a_0 = b_0 = c_0 = 0$ である。これを解けばよい。
解
z 変換
ja.wikipedia.org
$\mathcal{Z}[x_n] = X(z)$ に対して、$\mathcal{Z}[x_{n-1}] = z^{-1} X(z)$ であることを利用して、先の連立漸化式の辺々を z 変換すると、$$
\begin{empheq}[left=\empheqlbrace]{align}
A(z) &= z^{-1} A(z) + z^{-1} B(z) \\
B(z) &= z^{-1} A(z) + z^{-1} C(z) \\
C(z) &= z^{-1} B(z) + z^{-1} C(z) + \mathcal{Z}[n]
\end{empheq}$$である。これを変形すると、$$
\begin{empheq}[left=\empheqlbrace]{align}
A(z) &= \frac{1}{z-1} B(z) \\
B(z) &= \frac{z}{(z+1) (z-2)} \mathcal{Z}[n] = \frac{z^2}{(z-1)^2 (z+1) (z-2)} \\
C(z) &= A(z) + \frac{z}{z-1} \mathcal{Z}[n]
\end{empheq}
$$が得られる。
逆 z 変換
$B(z)$ の式の最右辺を部分分数分解してみる。
$$\begin{align} B(z)
&= \frac{z^2}{(z-1)^2 (z+1) (z-2)} \\
&= z \qty[ \frac{z}{(z-1)^2 (z+1) (z-2)} ] \\
&= z \qty[ -\frac{1}{2} \frac{1}{(z-1)^2} -\frac{3}{4} \frac{1}{z-1} + \frac{1}{12}\frac{1}{z+1} + \frac{2}{3}\frac{1}{z-2} ] \\
&= -\frac{1}{2} \frac{z}{(z-1)^2} -\frac{3}{4} \frac{z}{z-1} + \frac{1}{12}\frac{z}{z+1} + \frac{2}{3}\frac{z}{z-2}\ \\
\end{align}$$
この両辺を逆 z 変換する。
$$\begin{align} \mathcal{Z}^{-1}[B(z)]
&= \mathcal{Z}^{-1} \qty [-\frac{1}{2} \frac{z}{(z-1)^2} -\frac{3}{4} \frac{z}{z-1} + \frac{1}{12} \frac{z}{z+1} + \frac{2}{3} \frac{z}{z-2} ] \\
&= -\frac{1}{2} n -\frac{3}{4} 1^n + \frac{1}{12} (-1)^n + \frac{2}{3} 2^n
\end{align}$$
これが $b_n$ に等しいので、$$b_n = \frac{1}{12} \qty( -6n-9+(-1)^n+2^{n+3} )$$となる。また、$$A(z) = \frac{1}{z-1} B(z)$$の両辺を逆 z 変換する。
$u(n)$ は単位ステップ関数とすると、$$\frac{z}{z-1} = \mathcal{Z}[u(n)]$$であり、$$\frac{1}{z-1} = z^{-1} \mathcal{Z}[u(n)] = \mathcal{Z}[u(n-1)] $$であることを考慮すると、畳み込みを直接計算することで、$$
\begin{align} a_n
&= \mathcal{Z}^{-1} \qty[ \frac{1}{z-1} B(z) ] \\
&= \mathcal{Z}^{-1} \qty[ \frac{1}{z-1} ] * \mathcal{Z}^{-1}[B(z)] \\
&= u(n-1) * b_n \\
&= \sum_{m=0}^\infty u(m-1) b_{n-m} \\
&= \sum_{m=1}^{n-1} b_{n-m} \\
&= \sum_{k=1}^{n-1} b_k \\
&= \frac{1}{12} \sum_{k=1}^{n-1} \qty( -6k-9+(-1)^k+2^{k+3} ) \\
&= \frac{1}{24} \qty( -6n^2-12n-15-(-1)^n+2^{n+4} )
\end{align}
$$である。また、$C(z)$ の逆変換について、$$
\begin{align} c_n
&= a_n + \mathcal{Z}^{-1} \qty[ \mathcal{Z}[u(n)] \mathcal{Z}[n] ] \\
&= a_n + u(n)*n \\
&= a_n + \sum_{m=0}^\infty u(m) (n-m) u (n-m) \\
&= a_n + \sum_{k=1}^n k \\
&= a_n + \frac{1}{2}n(n+1) \\
&= \frac{1}{24} \qty( -6n^2-12n-15-(-1)^n+2^{n+4} ) + \frac{1}{2}n(n+1) \\
&= \frac{1}{24} \qty( 6n^2-15-(-1)^n+2^{n+4} )
\end{align}
$$となる。
以上をまとめると、$$
\begin{empheq}[left=\empheqlbrace]{align}
a_n &= \frac{1}{24} \qty( -6n^2-12n-15-(-1)^n+2^{n+4} ) \\
b_n &= \frac{1}{12} \qty( -6n-9+(-1)^n+2^{n+3} ) \\
c_n &= \frac{1}{24} \qty( 6n^2-15-(-1)^n+2^{n+4} )
\end{empheq}
$$が解である。
別解
連立漸化式の行列表記
先の連立漸化式$$
\begin{empheq}[left=\empheqlbrace]{align}
a_n &= a_{n-1}+b_{n-1} \\
b_n &= a_{n-1}+c_{n-1} \\
c_n &= b_{n-1}+c_{n-1}+n
\end{empheq}$$を行列を用いて表すことにすると、$$
\mqty[a_n \\ b_n \\ c_n ] =
\mqty[1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1]
\mqty[a_{n-1} \\ b_{n-1} \\ c_{n-1} ] +
\mqty[0 \\ 0 \\ n]
$$となる。ここで、$$
\vb*{x}_n=\mqty[a_n \\ b_n \\ c_n ],
M=\mqty[1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1],
\vb*{y}_n=\mqty[0 \\ 0 \\ n ]
$$とおくと、$$\vb*{x}_n = M \vb*{x}_{n-1} + \vb*{y}_n, \quad \vb*{x}_0 = \vb*{0}$$という漸化式になる。
漸化式の展開
$$\begin{empheq}[left=\empheqlbrace]{align}
\vb*{x}_1 &= M \vb*{x}_{0} + \vb*{y}_1 \\
&= \vb*{y}_1 \\
\vb*{x}_2 &= M \vb*{x}_{1} + \vb*{y}_2 \\
&= M \vb*{y}_1 + \vb*{y}_2 \\
\vb*{x}_3 &= M \vb*{x}_{2} + \vb*{y}_3 \\
&= M (M \vb*{y}_1 + \vb*{y}_2) + \vb*{y}_3 \\
&= M^2 \vb*{y}_1 + M \vb*{y}_2 + \vb*{y}_3 \\
&\vdots \\
\vb*{x}_n &= M \vb*{x}_{n-1} + \vb*{y}_n \\
&= M (M \vb*{x}_{n-2} + \vb*{y}_{n-1}) + \vb*{y}_n \\
&= M \qty(M (M \vb*{x}_{n-3} + \vb*{y}_{n-2}) + \vb*{y}_{n-1}) + \vb*{y}_n \\
&= \cdots \\
&= M^{n-1} \vb*{y}_{1} + M^{n-2} \vb*{y}_{2} + M^2 \vb*{y}_{n-2} + M \vb*{y}_{n-1} + \vb*{y}_n \\
&= \sum_{k=1}^n M^{n-k} \vb*{y}_k
\end{empheq}$$
ここで、$M^n$ の $k$ 列目を $\vb*{m}^{(n)}_k$ と書くことにすると、$$
\begin{align}
M^{n-k} \vb*{y}_k
&= \mqty[\vb*{m}^{(n-k)}_1 & \vb*{m}^{(n-k)}_2 & \vb*{m}^{(n-k)}_3]
\mqty[0 \\ 0 \\ k] \\
&= k \vb*{m}^{(n-k)}_3
\end{align}$$となるから、$$\vb*{x}_n = \sum_{k=1}^n k \vb*{m}^{(n-k)}_3$$となる。
対角化
$M$ を対角化することにより、$M^n$ を求める。
例えば、
$$D=\mqty[-1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2],
P=\mqty[1 & 1 & 1 \\ -2 & 0 & 1 \\ -1 & -1 & 1],
P^{-1}= \frac{1}{6} \mqty[1 & -2 & 1 \\ 3 & 0 & -3 \\ 2 & 2 & 2]$$が得られ、$$
\begin{align} M^n
&= P D^n P^{-1} \\
&= \frac{1}{6} \mqty[1 & 1 & 1 \\ -2 & 0 & 1 \\ -1 & -1 & 1]
\mqty[(-1)^n & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2^n]
\mqty[1 & -2 & 1 \\ 3 & 0 & -3 \\ 2 & 2 & 2] \\
&=\frac{1}{6} \mqty[\cdot & \cdot & -3+(-1)^n+2^{n+1} \\
\cdot & \cdot &-2(-1)^n+2^{n+1} \\
\cdot & \cdot &3+(-1)^n+2^{n+1}]
\end{align}
$$となる。これにより、$$
\begin{align} \vb*{x}_n
&= \sum_{k=1}^n k \vb*{m}^{(n-k)}_3 \\
&= \frac{1}{6} \sum_{k=1}^n k \mqty[
-3+(-1)^{n-k}+2^{n-k+1} \\
-2(-1)^{n-k}+2^{n-k+1} \\
3+(-1)^{n-k}+2^{n-k+1}
] \\
&= \frac{1}{6} \sum_{k=1}^n \mqty[
-3k+(-1)^n k (-1)^k+2^{n+1} k \left( \frac{1}{2} \right)^k \\
2(-1)^{n+1} k (-1)^k +2^{n+1} k \left( \frac{1}{2} \right)^k \\
3k+(-1)^n k (-1)^k+2^{n+1} k \left( \frac{1}{2} \right)^k \\
] \\
&= \frac{1}{6} \qty( \mqty[ -3 \\ 0 \\ 3] \sum_{k=1}^n k + \mqty[(-1)^n \\ 2(-1)^{n+1} \\ (-1)^n]
\sum_{k=1}^n k (-1)^k +\mqty[2^{n+1} \\ 2^{n+1} \\ 2^{n+1}]
\sum_{k=1}^n k \qty( \frac{1}{2} )^k)
\end{align}$$となる。
等差×等比タイプの和
$ r \ne 1$ のとき、$$S_n = \sum_{k=1}^n k r^k$$とおくと、$$
\begin{empheq}[left=\empheqlbrace]{align}
S_n &= r + 2r^2 + 3r^3 + \cdots + n r^n \\
r S_n &= r^2 + 2r^3 + 3r^4 + \cdots + (n-1) r^n + n r^{n+1}
\end{empheq}$$より、$$
\begin{align} (1-r) S_n
&= r + r^2 + r^3 + \cdots + r^n - n r^{n+1} \\
&= \frac{r(1-r^n)}{1-r} - n r^{n+1}
\end{align}$$だから、$$S_n = \frac{r(1-r^n)}{(1-r)^2} - \frac{n r^{n+1}}{1-r}$$となる。
これにより、$$\sum_{k=1}^n k(-1)^k = \frac{-1+(-1)^n}{4} - \frac{n (-1)^{n+1}}{2}$$また、$$\sum_{k=1}^n k \qty(\frac{1}{2} )^k = 2 \qty(1-\frac{1}{2^n} ) - \frac{n}{2^n}$$となる。
これらを利用して整理すると、$$\vb*{x}_n = \mqty[
\frac{1}{24} \qty( -6n^2-12n-15-(-1)^n+2^{n+4} ) \\
\frac{1}{12} \qty( -6n-9+(-1)^n+2^{n+3} ) \\
\frac{1}{24} \qty( 6n^2-15-(-1)^n+2^{n+4} )
]$$という同様の解が得られる。
点数表
| $n$ | $a_n$ | $b_n$ | $c_n$ |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 2 | 0 | 1 | 3 |
| 3 | 1 | 3 | 7 |
| 4 | 4 | 8 | 14 |
| 5 | 12 | 18 | 27 |
| 6 | 30 | 39 | 51 |
| 7 | 69 | 81 | 97 |
| 8 | 150 | 166 | 186 |
| 9 | 316 | 336 | 361 |
| 10 | 652 | 677 | 707 |
| 11 | 1329 | 1359 | 1395 |
| 12 | 2688 | 2724 | 2766 |
| 13 | 5412 | 5454 | 5503 |
| 14 | 10866 | 10915 | 10971 |
| 15 | 21781 | 21837 | 21901 |
| 16 | 43618 | 43682 | 43754 |
| 17 | 87300 | 87372 | 87453 |
| 18 | 174672 | 174753 | 174843 |
| 19 | 349425 | 349515 | 349615 |
| 20 | 698940 | 699040 | 699150 |
| 21 | 1397980 | 1398090 | 1398211 |
| 22 | 2796070 | 2796191 | 2796323 |
| 23 | 5592261 | 5592393 | 5592537 |
所感
別解はロジックはエレガントなものの、いざやってみると手計算がつらすぎるので実用的ではない気がした。また、ハノイの塔が門松の竹柱と鏡餅のセットに似ている気がするので、縁起のよい正月遊びとして推していきたい。