
さて、観覧車のゴンドラは振り子のようになっていて、理論上は観覧車の回転によってゴンドラが揺れるはずである。この運動を表す運動方程式を求めたい。
いや、これはモチベーションとしては後付けであって、二重振り子に興味を持ち、これは非常にカオスなのでもうちょっと秩序のある振り子の運動を調べたいというきっかけから、支点を周期的に動かせばいいのではということになり、等速円運動くらいがいいよね、という過程のもとであり、これはすなわち観覧車とゴンドラのモデル化だよね、という話なのだ。
それはさておき、さっそく運動方程式を作る。ラグランジュの方程式だ。解析力学。
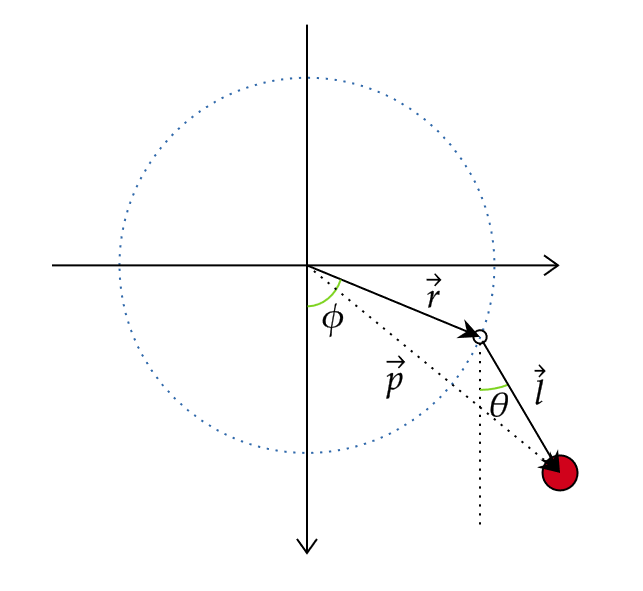
鉛直面があり、そこに適当な原点を中心とする適当な半径 $r$ の円がある。位置ベクトルを $\vec r$ とする点が円周上を動くとする。その点を支点として長さ $l$ の理想的な棒がぶら下がっており、その先には質量 $m$ の質点がある。この質点の鉛直面上での運動を考える。例によって摩擦や空気抵抗はないものとする。
支点から質点へのベクトルを $\vec l$ とする。すると、質点の位置ベクトル $\vec p$ は$$\vec p = \vec r + \vec l$$で表される。$\vec p$ だけど運動量ではない。
ここで質点の運動エネルギー $T$ を求めたい。縦軸を鉛直下向きを正の向きとして、縦軸と $\vec r$ のなす角を $\phi$、縦軸と $\vec l$ のなす角を $\theta$ とする。これらは時刻 $t$ の関数であり、特に一定の角速度 $\omega$ を用いて $\phi=\omega t$ となる等速円運動を考える。また、$\theta$ こそが最終的に求めたい関数であり、一般化座標として用いるものである。
$$\begin{align}
T &= \frac{m}{2} \dot{\vec p}^2 \\
&= \frac{m}{2} \qty( \dot{\vec r} + \dot{\vec l} )^2 \\
&= \frac{m}{2} \qty( \dot{\vec r}^2 + 2 \dot{\vec r} \cdot \dot{\vec l} + \dot{\vec l}^2 ) \\
&= m \qty( \frac{1}{2}r^2 \dot{\phi}^2 + rl\dot{\phi}\dot{\theta} \cos( \phi-\theta ) + \frac{1}{2}l^2\dot{\theta}^2 )
\end{align}$$
こうだ。$\dot{\vec l}$ は $\vec l$ と垂直だが、$\dot \theta$ の正負によって向きが変わることに注意して内積をとりたいところ。
さらに、ポテンシャル $U$ を求めたい。$\phi=0$ かつ $\theta=0$ のときに最小となるように適当に定める。
$$\begin{align}
U &=-mg \qty( \vec p の鉛直下向き成分 ) \\
&=-mg \qty( r \cos \phi + l \cos \theta )
\end{align}$$
さて、これらを用いてラグランジアン $L=T-U$ を求める。
$$L =m \qty( \frac{1}{2}r^2 \dot{\phi}^2 + rl\dot{\phi}\dot{\theta} \cos( \phi-\theta ) + \frac{1}{2}l^2\dot{\theta}^2 ) + mg \qty(r \cos \phi + l \cos \theta )$$
あとはラグランジアンを微分したりしたやつを求める作業。まずは $\dot \theta$ で偏微分。
$$\pdv{L}{\dot{\theta}} = m \qty( rl\dot{\phi} \cos( \phi-\theta ) + l^2 \dot{\theta} ) $$
これの時間微分。
$$\begin{align}
\dv{t} \qty( \pdv{L}{\dot{\theta}} )
&= m \qty[ rl \qty( \ddot{\phi} \cos( \phi-\theta ) - \dot{\phi}\qty( \dot{\phi}-\dot{\theta} ) \sin( \phi-\theta )) +l^2\ddot{\theta} ] \\
&= m \qty( rl \qty( \dot{\phi}\dot{\theta}-\dot{\phi}^2 ) \sin( \phi-\theta ) +l^2\ddot{\theta} )
\end{align}$$
$\phi = \omega t$ であったから、$\ddot \phi = \dot \omega = 0$ である。別に、$\theta$ で偏微分。
$$\pdv{L}{\theta}= m \qty( rl\dot{\phi}\dot{\theta} \sin( \phi-\theta ) - gl \sin \theta )$$
はい。ここからラグランジュの運動方程式 $\dv{t}\qty( \pdv{L}{\dot{\theta}} )-\pdv{L}{\theta}=0$ を作る。
$$\begin{align}
\dv{t}\qty( \pdv{L}{\dot{\theta}} )-\pdv{L}{\theta} &= m \qty( rl \qty( \dot{\phi}\dot{\theta}-\dot{\phi}^2 ) \sin( \phi-\theta ) +l^2\ddot{\theta} - rl\dot{\phi}\dot{\theta} \sin( \phi-\theta ) + gl \sin \theta ) \\
&= m \qty( -rl \dot{\phi}^2 \sin( \phi-\theta ) +l^2\ddot{\theta} + gl \sin \theta ) \\
&= m \qty( -rl \omega^2 \sin(\omega t-\theta ) +l^2\ddot{\theta} + gl \sin \theta ) = 0
\end{align}$$
よって、次の運動方程式を得る。
$$\ddot{\theta} = \frac{r \omega^2}{l} \sin(\omega t-\theta ) - \frac{g}{l} \sin \theta $$
普通の単振り子の強制振動の式に似た形。ぐわんぐわん揺らしたいので、微小振動どころの話ではなく、$\theta \approx 0$ とした近似は使えない。解析的には解けなそう。
ならば数値計算だ。SageMath を使ってルンゲ・クッタ法による数値解を出してもらう。ただ、$\theta (t)$ の概形を見てもあまり面白くないので、条件を変えながら実際の振り子の動きを見てみようではないか。とりあえず $\omega$ と $\theta(0)$ のバリエーションで $\vec l$ の動き方の図を出した。各種定数や初期値を各図の左上に表示してある。w は $\omega$ のつもり。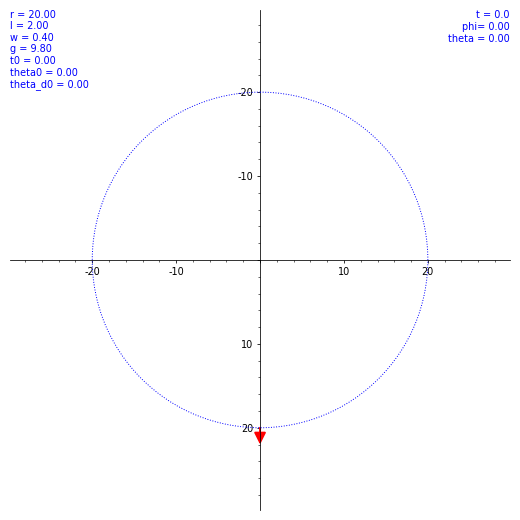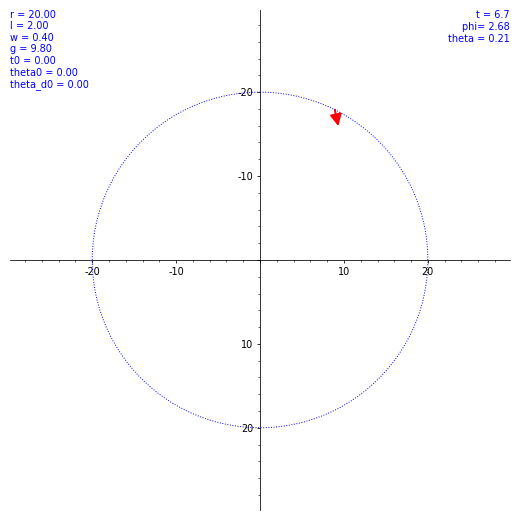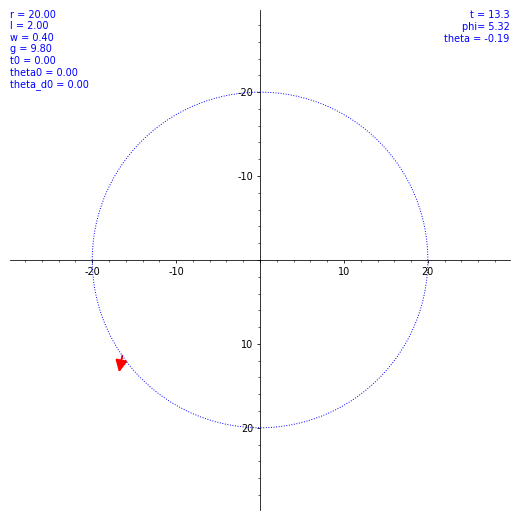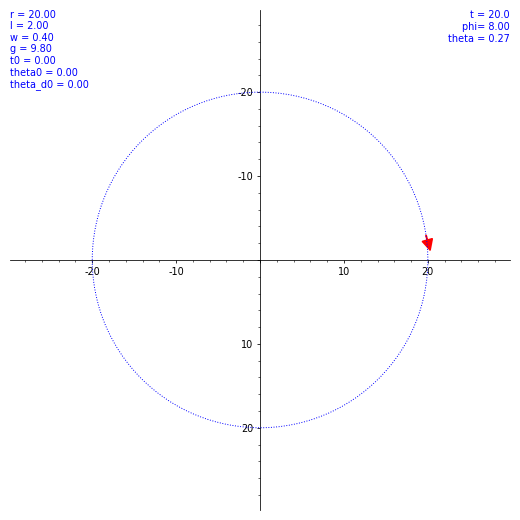
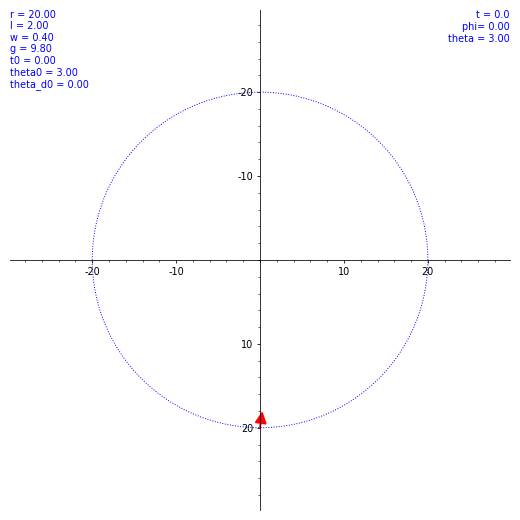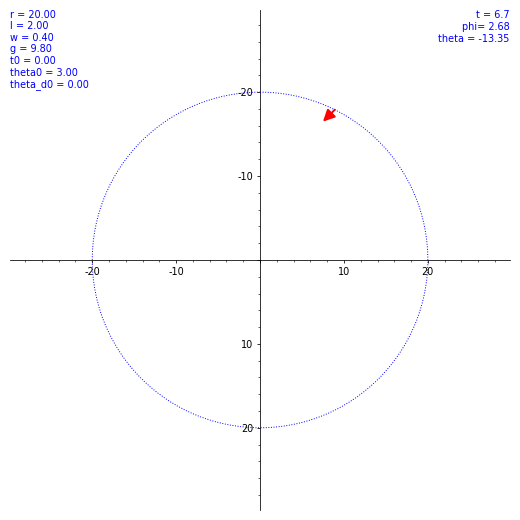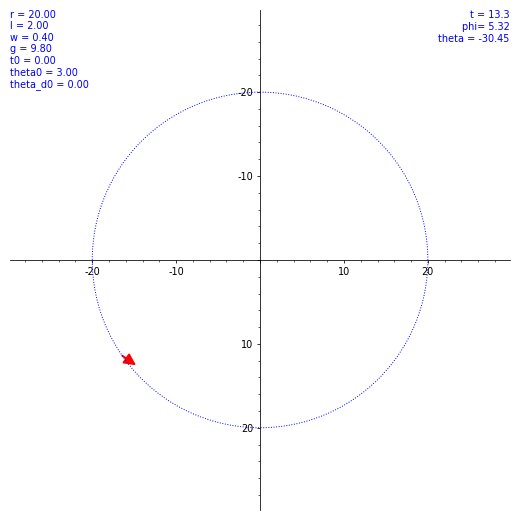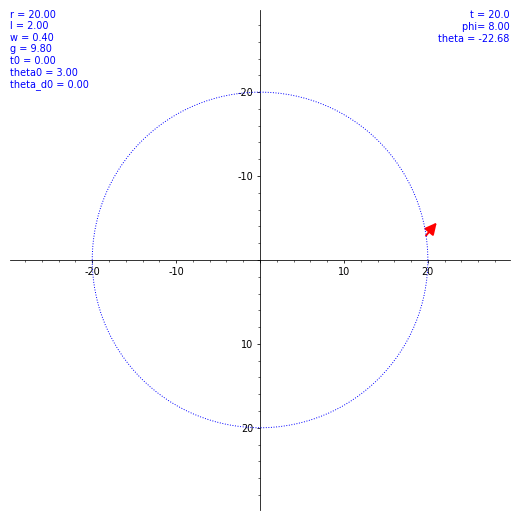
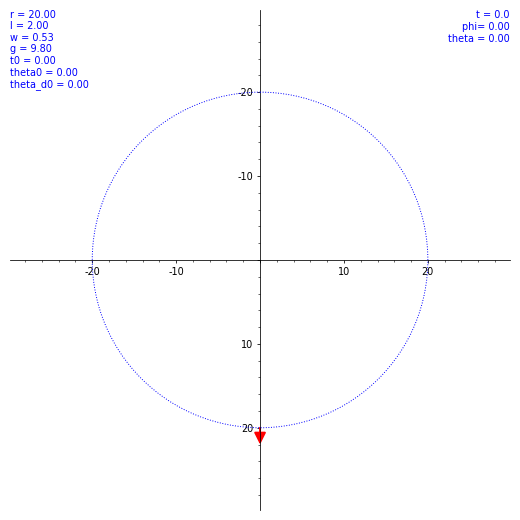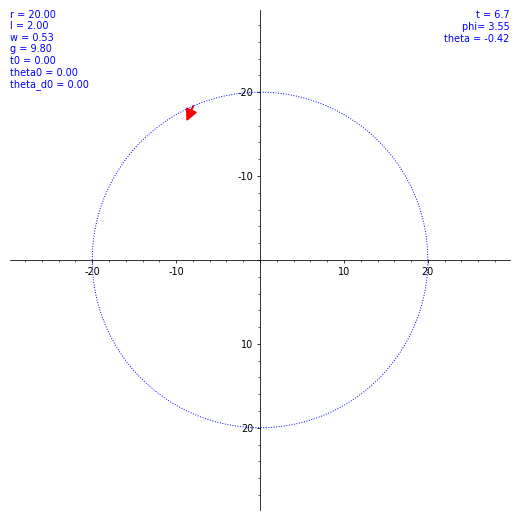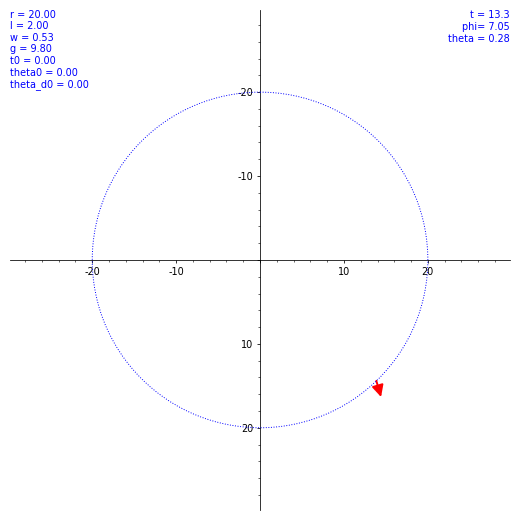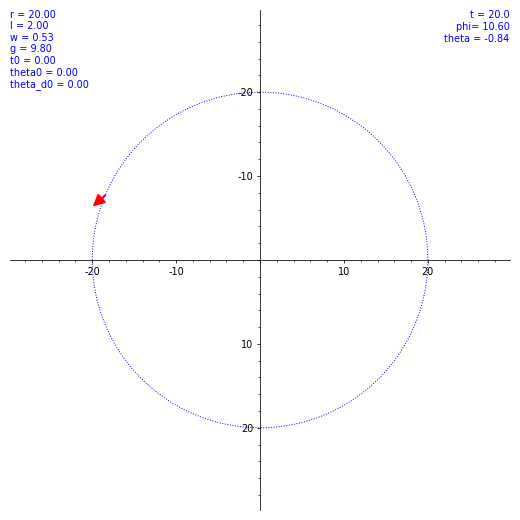
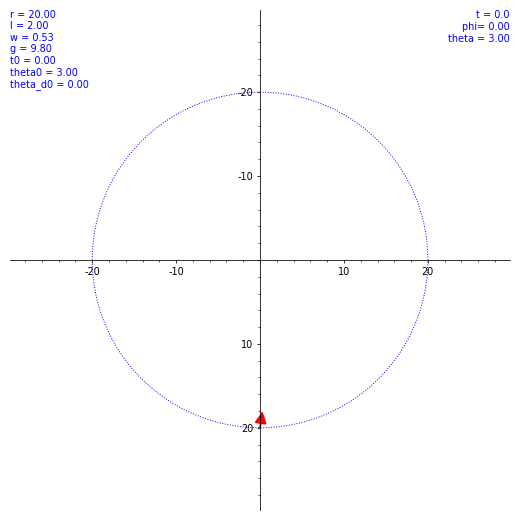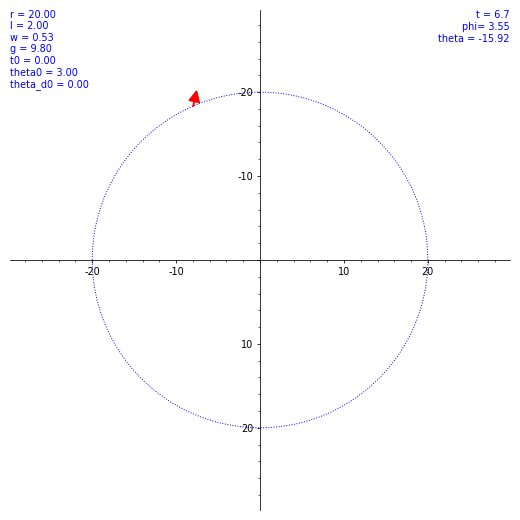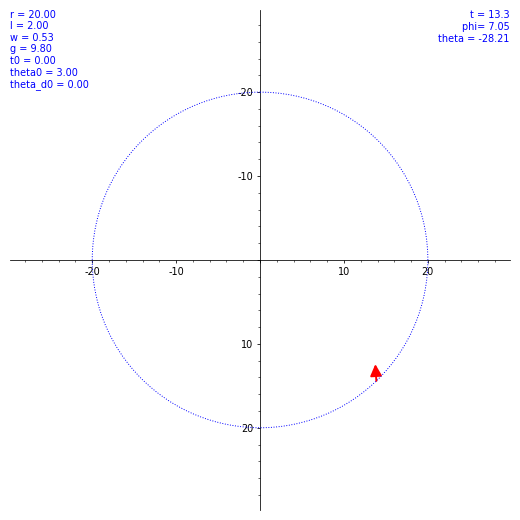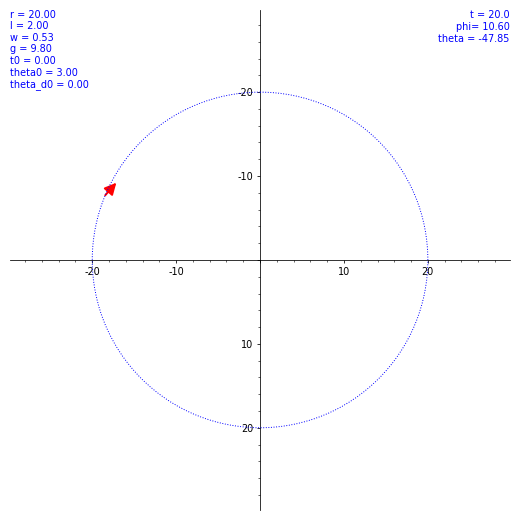
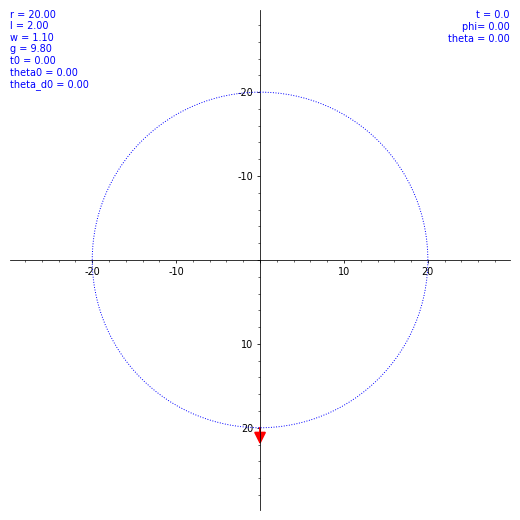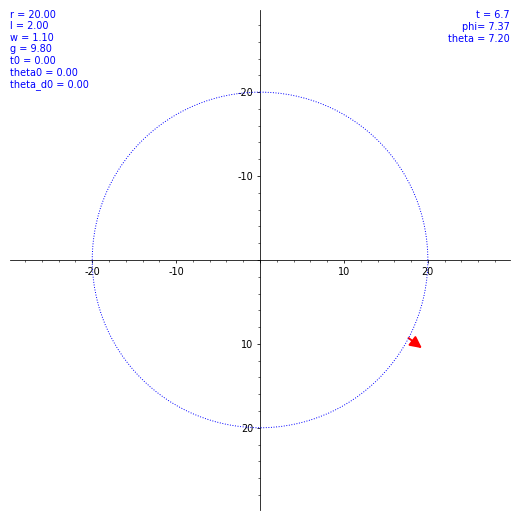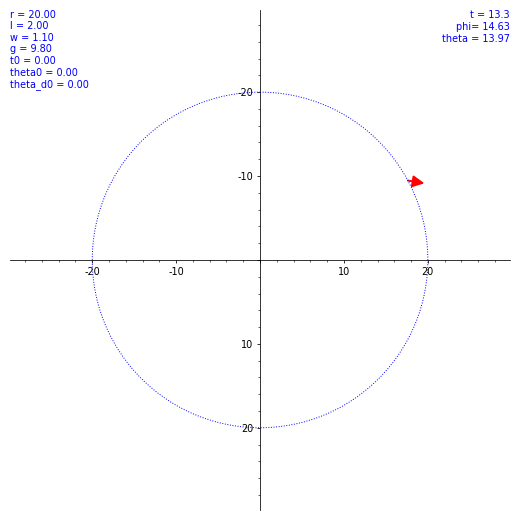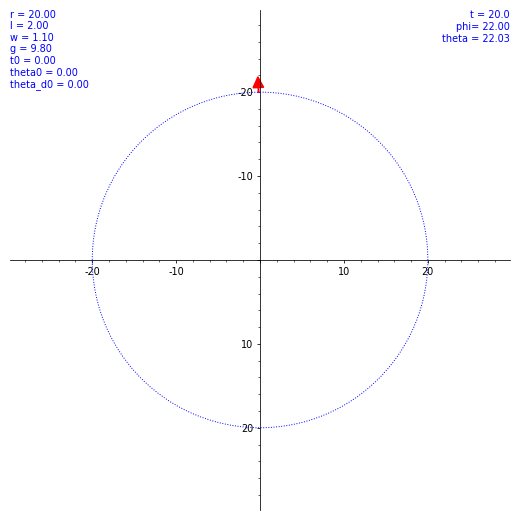
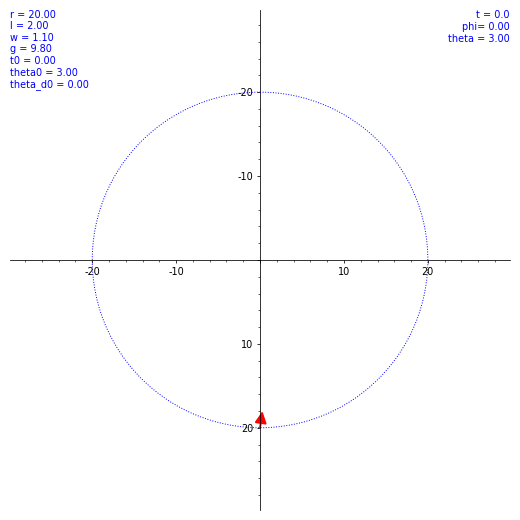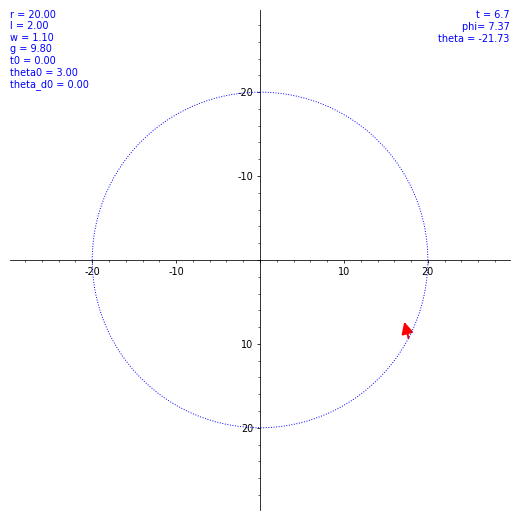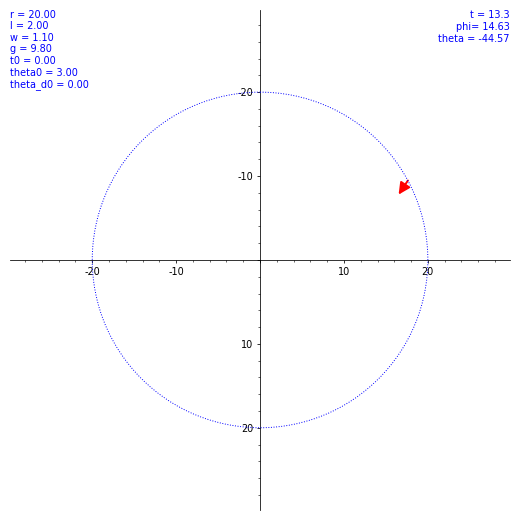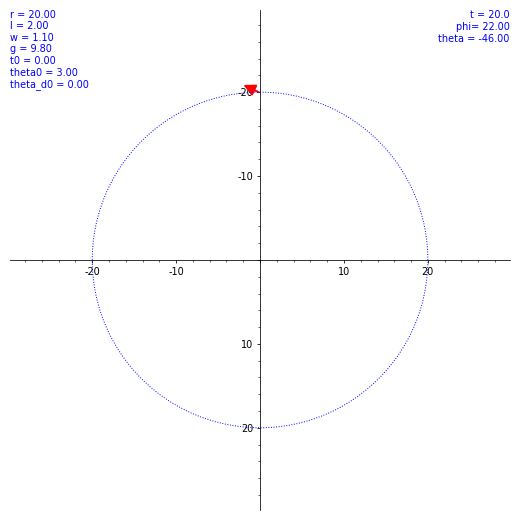
気持ちよくぐわんぐわん揺れてくれたが、実際の乗客は気持ち悪くなること必至。
円の半径よりも棒が適度に長いほうが面白いかな。

今回使用した SageMath のコードを書いておく。
def f(r,l,w,g=9.8,t0=0,theta0=0,theta_d0=0): (t,theta,theta_d)=var('t theta theta_d') A=desolve_system_rk4([theta_d,r*w*w*sin(w*t-theta)/l-g*sin(theta)/l], [theta,theta_d], ics=[t0,theta0,theta_d0], ivar=t, end_points=20) coord_lim = (r+l)*1.3 legend1='r = %.2f\nl = %.2f\nw = %.2f\ng = %.2f'%(r,l,w,g) legend2='t0 = %.2f\ntheta0 = %.2f\ntheta_d0 = %.2f'%(t0,theta0,theta_d0) def coord_r(t): return r*sin(w*t_),r*cos(w*t_) def coord_p(t,th): return vector(coord_r(t))+vector((l*sin(th),l*cos(th))) an=animate([ text(legend1+'\n'+legend2,(0,1),axis_coords=True,vertical_alignment='top',horizontal_alignment='left')+ text('t = %.1f\nphi= %.2f\ntheta = %.2f\n'%(t_,w*t_,theta_),(1,1),axis_coords=True,vertical_alignment='top',horizontal_alignment='right')+ circle((0,0),r,linestyle=':')+ arrow(coord_r(t_),coord_p(t_,theta_),color='red') for t_,theta_,_ in A], xmin=-coord_lim,xmax=coord_lim,ymin=coord_lim,ymax=-coord_lim,aspect_ratio=1,figsize=10,dpi=70) an.gif(delay=10,savefile=(legend1+legend2).replace(' = ','_').replace('\n',''),show_path=True)
